Dynamic Programming

What is this ?

Dynamic is neither focusing on pure programming neither involves dynamism in some way, it is actually a buzzword created to refer to a methodology invited by applied mathematician Richard Bellman.

Dynamic programming is a methodology that provides guidelines to reduce a problem’s complexity, which you mainly do by dividing it into sub-problems and by caching the intermediate results. Doing so will allow us to use solutions to problems that we know the approach, and will also allow us to waste less time and memory through the caching of redundant calculations.

Tldr

”Divide and conquer!”

Caching

The process of caching/proxying/memoisation refers to the process of keeping the results of a function depending of the input value. This allows us to avoid re-running the function in calculations that might generate redundant function calls.

The Fibonacci suite is the prime example of this, let’s take at the usual implementation of it:

def fibonacci(n) do 
  case n do 
    _ when n < 2 -> n
    _ -> fibonacci(n - 1) + fibonacci(n - 2)
end

When you decompose the calls of this function, here is the calling tree you get:

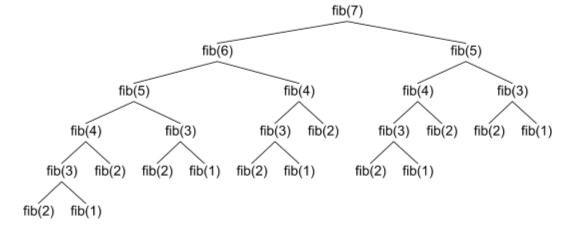
Don’t you see something shocking? Besides the number of calls that have been made for such a small input, the quantity of redundant function calls you do is insanely high.

By caching the results of fibonacci(n) we would cut down the calling tree like this:

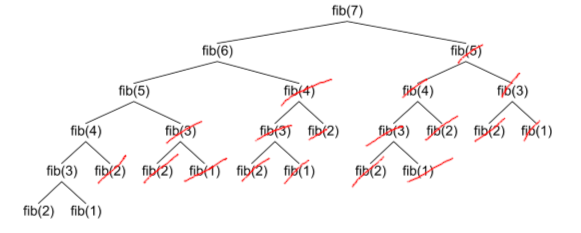
And as you can imagine, you greatly reduce the resourced used by the function.

Complexity wise...

What we effectively have here is a recursive function that itself two times for each input $n$, giving it effectively a exponential complexity of $\mathcal{O}(2^n)$ Now with caching we simplified our tree by trimming one of the two recursive calls bringing down it’s complexity to $\mathcal{O}(n)$